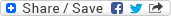
Many of the modern motor testers today utilize a spectral analysis tool known as a Fast Fourier Transform or FFT for short. When reading up on motor test theory, this is a topic that is mentioned often and repeated almost as often, but when pressed for an explanation many folks find themselves scratching their heads. They’ve seen an FFT on their tester, and probably know how to interpret the data it provides, but may still be at a loss as to how it’s derived.

When we think of voltage, many people think of a numerical value, for example, 480VAC. This value is actually the Root Mean Squared (RMS) value of the voltage. Those of us familiar with oscilloscopes have seen voltage waveforms, but those are measured by another method; peak-to-peak. In peak-to-peak measurement of voltage waveforms, the value measured is from the top of the positive going sine wave to the bottom of the negative going sine wave. This value is actually greater than RMS value. RMS is .707 x Volts peak.

When we measure voltage in this way, we’re viewing the voltage waveform in a time domain. The distance from one side of the “o’scope” screen to the other is measured in a unit of time measurement. Cycles, milliseconds, whichever. That gives us a look at the voltage in one dimension only. The Fast Fourier Transform allows us to view voltage and current waveforms from another direction; from the perspective of frequency. This view allows us to see distortions in the waveforms in a different presentation, allowing us to pinpoint how these distortions occur in relation to one another.

Think of it this way, when viewing voltage or current waveforms in the time domain, like with an oscilloscope, it’s as if you’re standing on the side of the road watching the waveform move past you. In the frequency domain, like in an FFT, it’s more like standing on a bridge over the road, watching the waveform move beneath you. You get to see it from a completely different perspective, and the things that aren’t readily visible in the time domain are more easily detected in the frequency domain that the FFT provides.

So, when you apply your motor test instrument, you’re looking at the same voltage or current that you would with an oscilloscope, a voltmeter or a clamp-on ammeter, you’re just seeing it from a different view. You still have the benefit of being able to view RMS values of both voltage and current in other presentations of the tester, so you’re able to see the entire voltage and current picture for better analysis of your critical motor data.

An FFT is looking at a signal in the frequency domain as opposed to the time domain. Imagine traffic passing you as you stand by the side of the road, facing the roadway. Cars pass from your left to your right. That’s the time domain, the past to the left, future to the right. Now imagine a bridge that goes over the traffic. If you walk onto the bridge and stand above the traffic, looking down at it, cars move from top to bottom of your field of view. That’s like the frequency domain. An FFT is an algorithm for looking at data from a different perspective.